53. Связь между диаграммами Вирта и праволинейными грамматиками. Преобразование правой рекурсии в итерацию.
Использование диаграмм Вирта для непосредственного написания программы позволяет говорить о том, что, при наличии праволинейной грамматики, можно не строить конечный автомат, а преобразовать исходную грамматику в диаграммы Вирта. Непосредственное представление праволинейной грамматики диаграммами Вирта не вызывает каких-либо проблем (рис. 4.3), но полученный результат не позволяет переходить к написанию программы из-за наличия в правых частях правил нетерминалов.
В ряде случаев от нетерминалов можно избавиться простой подстановкой. Но, если в правиле имеется рекурсия, обычную подстановку осуществить не удастся. Однако можно воспользоваться тем, что в праволинейной грамматике допускается только правая рекурсия, которая легко заменяется итерацией.
Замена правой рекурсии на итерацию в диаграммах Вирта производится следующим простым способом:
· дуга, входящая в рекурсивно определяемый нетерминал, замыкается своим выходом на самое начало правила, образуя, таким образом, цикл;
- сам нетерминал, оказавшийся в подвешенном состоянии вычеркивается, а выходившая из него дуга убирается.
Пример на рис. 4.4: $IMAGE2$
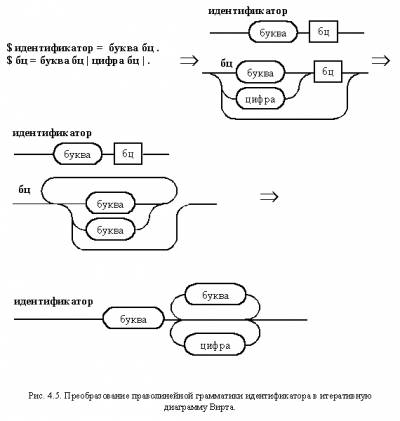
Он показывает возможность такого преобразования, исходя из следующих индуктивных рассуждений. Нетерминал A на первом шаге порождает терминальную цепочку x или терминальную цепочку y, за которой следует нетерминал A, из которого на следующем шаге можно породить терминальную цепочку x или терминальную цепочку y, за которой следует нетерминал A, из которого... Эти бесконечные рассуждения на тему "У попа была собака..." можно заменить одной структурированной фразой: Нетерминал A порождает терминальную цепочку y, повторяющуюся ноль или большее число раз, за которой следует терминальная цепочка x. На рис. 4.5 приведено преобразование в итеративную диаграмму Вирта правил праволинейной грамматики, описывающих идентификатор. После избавления от лишних нетерминалов мы получаем хорошо знакомый результат.
|