52. Связь между диаграммой Вирта и конечным автоматом
Построение конечного автомата можно осуществить также с использованием ряда грамматик с левой рекурсией и диаграмм Вирта. На практике, вместо праволинейной грамматики, удобнее использовать диаграммы Вирта. Они намного нагляднее при описании правил. Кроме этого, между диаграммами Вирта, не содержащими нетерминалов, и конечными автоматами существует однозначное соответствие. Практически это два эквивалентных способа представления одной модели, которая одновременно может служить как механизмом порождения, так и механизмом распознавания. Конечный автомат, эквивалентный диаграмме Вирта, состоящей только из терминалов, строится следующим образом:
1. Начальная дуга диаграммы преобразуется в начальное состояние конечного автомата.
2. Конечная дуга диаграммы образует заключительное состояние конечного автомата.
3. Выходы отдельных дуг, соединяющих символы, и точки ветвления остальных дуг диаграммы образуют множество остальных состояний конечного автомата.
4. Конечные состояния диаграммы являются допускающими состояниями конечного автомата.
5. Терминальный символ диаграммы Вирта, расположенный между дугами, преобразуется в связь между соответствующими состояниями, помеченную входным символом, равным этому терминалу.
6. Связи, обеспечивающие переход в допускающие состояния, помечаются множеством оставшихся символов. Это множество не пересекается с множеством символов, обеспечивающих другие переходы из текущего в другие состояния (обозначены как "прочие").
Построение конечного автомата в соответствии с данными правилами можно рассмотреть на примере описания идентификатора. Диаграмма Вирта для идентификатора и полученный по ней конечный автомат приведены на рис. 4.1. 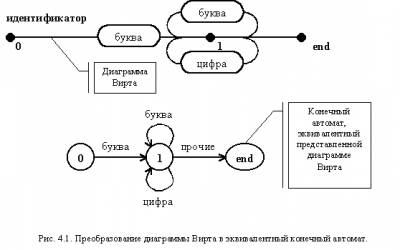
Для наглядности на дугах отмечены точки, соответствующие состояниям конечного автомата. Они обозначены теми же номерами, что и состояния. Заключительное состояние отмечено меткой "end". Следует еще раз отметить, что буква и цифра на диаграмме рассматриваются как терминалы, так как эти понятия формируются транслитератором.
Диаграммы Вирта могут использоваться и для того, чтобы минимизировать общее представление правил, что соответствует методам минимизации, применяемым к конечным автоматам. Эта минимизация осуществляется за счет объединения одинаковых подграфов диаграмм. Пример возможной минимизации понятия "идентификатор представлен на рис. 4.2.
Следует отметить, что не всегда минимизация диаграммы Вирта ведет к минимизации соответствующего ей конечного автомата. Приведенный рисунок показывает, что, несмотря на сокращение общего числа символов, разметка, соответствующая состояниям конечного автомата, осталась неизменной.
Наличие однозначного и легко понятного соответствия между диаграммами Вирта и конечными автоматами позволяет не строить последние, а переходить к НАПИСАНИЮ программы лексичского анализатора непосредственно от диаграмм Вирта. Это сокращает технологическую цепочку, связывающую формальное описание элементов языка программирования и их программную реализацию.
|